Сайт-визитка

РЕШЕБНИК МОРДКОВИЧА

Уважаемые школьники и студенты. Если уж вы зашли сюда в поисках решебника, будьте так добры, напишите в гостевой книге отзыв - что искали, нашли или нет, помогло или нет. Особенно если не нашли, или нашли, но не то. Я попытаюсь добавить интересующий вас решебник на сайт.
Пока решебник не закончен. Я еще нахожусь в процессе решения задач. Но вы можете существенно помочь процессу, кинув сообщение в гостевуху о том, что он вам нужен, и я работаю не зря. Это существенно поднимет мой боевой дух :)

1.13. а) Знаменатель должен быть не равен нулю $16x^2-49=0$ $16x^2=49$ $x^2=\frac{49}{16}$ $x_1=-\frac{7}{4}$ $x_2=\frac{7}{4}$ При этих x (ну или очень близких к ним) знаменатель будет стремиться к нулю, а наша функция к бесконечности. С одной стороны от корней - к плюс бесконечности, а с другой - к минус бесконечности. С другой стороны наша дробь не может быть равна нулю, так как чтобы дробь равнялась нулю - числитель должен равняться нулю. А он у нас равен единице. То есть мы получаем, что Область определения - все числа кроме x=-7/4 и x=7/4 Область значений - все числа кроме y=0 Продемонстрируем это Видно что при x=+-7/4 функция не существует, а также не существует точки, где y=0 б) Выражение под корнем должно быть больше или равно нулю $x^2+4x+3\geq0$ Решим уравнение $x^2+4x+3=0$ $D=b^2-4ac=16-4*1*3=4$ $x_1=\frac{-b-\sqrt{D}}{2a}=\frac{-4-2}{2}=-3$ $x_2=\frac{-b+\sqrt{D}}{2a}=\frac{-4+2}{2}=-1$ Так как коэффициент при x^2 больше нуля, то ветви параболы направлены вверх, и она больше нуля при x меньше (или равном) -3 и при x больше (или равном) -1 Определим область значений. Во-первых, корень всегда будет ноль или больше. С другой стороны - при x стремящемся к бесконечности, будет стремиться к бесконечности и подкоренное выражение, и сам корень. То есть мы получаем, что Область определения - x меньше или равно -3, либо x больше или равно -1 Область значений - 0 и все числа больше нуля Продемонстрируем это в) Знаменатель должен быть не равен нулю $9-25x^2=0$ $-25x^2=-9$ $25x^2=9$ $x^2=\frac{9}{25}$ $x_1=-\frac{3}{5}$ $x_2=\frac{3}{5}$ При этих x (ну или очень близких к ним) знаменатель будет стремиться к нулю, а наша функция к бесконечности. С одной стороны от корней - к плюс бесконечности, а с другой - к минус бесконечности. С другой стороны наша дробь не может быть равна нулю, так как чтобы дробь равнялась нулю - числитель должен равняться нулю. А он у нас равен единице. То есть мы получаем, что Область определения - все числа кроме x=-3/5 и x=3/5 Область значений - все числа кроме y=0 Продемонстрируем это Видно что при x=+-3/5 функция не существует, а также не существует точки, где y=0 г) Выражение под корнем должно быть больше или равно нулю $3x-x^2+18\geq0$ Решим уравнение $-x^2+3x+18=0$ $D=b^2-4ac=9-4*(-1)*18=81$ $x_1=\frac{-b-\sqrt{D}}{2a}=\frac{-3-9}{-2}=6$ $x_2=\frac{-b+\sqrt{D}}{2a}=\frac{-3+9}{-2}=-3$ 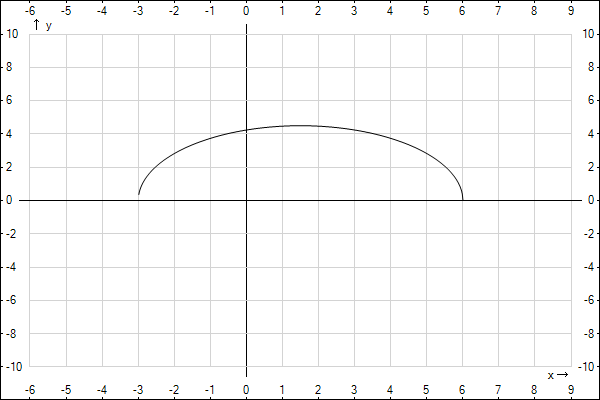Так как коэффициент при x^2 меньше нуля, то ветви параболы направлены вниз, и она больше нуля при x располагающимся между корнями, то есть при x от -3 до 6 (включая эти числа) Определим область значений. Во-первых, корень всегда будет ноль или больше. С другой стороны - в вершине параболы y будет максимально. Определим это максимальное значение: $x_v=\frac{-b}{2a}=\frac{-3}{-2}=1,5$ $y_v=-(1,5)^2+3*1,5+18=20,25$ $\sqrt{20,25}=4,5$ Итак, максимальное значение y=4,5 будет в точке x=1,5 То есть мы получаем, что Область определения - x от -3 до 6 (включая -3 и 6) Область значений - От нуля до 4,5 (включая 0 и 4,5) Продемонстрируем это

Хостинг от uCoz

МЕНЮ

РЕШЕБНИК МОРДКОВИЧА